Distribución hipergeométrica
Mira otros diccionarios:
Distribución hipergeométrica — Saltar a navegación, búsqueda Distribución hipergeométrica Función de distribución de probabilidad Parámetros Dominio … Wikipedia Español
Distribución de probabilidad — La distribución Normal suele conocerse como la campana de Gauss . En teoría de la probabilidad y estadística, la distribución de probabilidad de una variable aleatoria es una función que asigna a cada suceso definido sobre la variable aleatoria… … Wikipedia Español
Distribución t de Student — Función de densidad de probabilidad Función de distribución de pr … Wikipedia Español
Función error — Gráfica de la función error. En matemáticas, la función error (también conocida como función error de Gauss) es una función especial (no elemental) que se utiliza en el campo de la probabilidad, la estadística y las ecuaciones diferenciales… … Wikipedia Español
Funciones matemáticas — Anexo:Funciones matemáticas Saltar a navegación, búsqueda Contenido 1 Funciones Elementales 2 Funciones trascendentales 3 Funciones no elementales 4 … Wikipedia Español
Anexo:Funciones matemáticas — Este artículo o sección necesita referencias que aparezcan en una publicación acreditada, como revistas especializadas, monografías, prensa diaria o páginas de Internet fidedignas. Puedes añadirlas así o avisar … Wikipedia Español
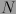 ,
, 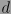 y
y  cuya función de probabilidad es:
cuya función de probabilidad es:
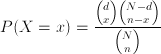 Aquí,
Aquí, 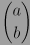 se refiere al coeficiente binomial, o al número de combinaciones posibles al seleccionar
se refiere al coeficiente binomial, o al número de combinaciones posibles al seleccionar 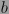 elementos de un total
elementos de un total 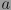 .
Esta distribución se refiere a un espacio muestra donde hay elementos de 2 tipos posibles. Indica la probabilidad de obtener un número de objetos
.
Esta distribución se refiere a un espacio muestra donde hay elementos de 2 tipos posibles. Indica la probabilidad de obtener un número de objetos  de uno de los tipos, al sacar una muestra de tamaño
de uno de los tipos, al sacar una muestra de tamaño  , de un total de
, de un total de 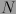 objetos, de los cuales
objetos, de los cuales 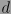 son del tipo requerido.
son del tipo requerido.